Phép nhân là một phần quan trọng trong chương trình toán học của học sinh. Vậy cấp số nhân là gì? công bội là gì? Làm thế nào để tính hệ cấp số nhân? Bài viết dưới đây chứa đựng những kiến thức thú vị liên quan.

Cấp số nhân là gì? Công bội là gì?
Cấp số nhân là một dãy số vô hạn hoặc hữu hạn thỏa mãn điều kiện vì số hạng thứ hai được gọi là số mũ. Mỗi số hạng bằng số hạng liền trước nó nhân với một số hạng không đổi. Số hạng không đổi này được gọi là cấp số nhân của cấp số nhân.
Công thức phục hồi:
Nếu (U n ) là số mũ với q là bội số thì ta có công thức:
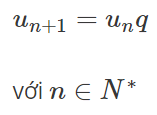
Ví dụ: Dãy số: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024,….là dãy số có phần tử đầu tiên là 1 với hệ số q = 2. => The sự thay đổi của cấp số nhân phụ thuộc vào giá trị của cấp số nhân q.
Hệ số q của hệ cấp số nhân (U1) được tính theo công thức:
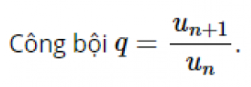
Ví dụ: Cho số mũ (Un) có (U1) = 4 và (U2) = 8. Tính hệ số q?
Trả lời: Tính số q = 8/4 = 2. (dùng công thức tính hệ số q)
Kết luận: q = 2.
Chú ý:
– Khi q = 0 thì số mũ có dạng: u1, 0, 0, …
– Khi q = 1 thì số mũ là dãy số không đổi có dạng: u1, u1, u1,…
– Khi q < 0 thì số mũ là dãy số không tăng, không giảm.
– Khi q > 0 và q < 1 thì số mũ là dãy số giảm dần.
– Khi q > 1 thì số mũ là dãy số tăng dần.
– Khi u1 = 0, với mọi q thì số mũ có dạng: 0, 0, 0,…
Ví dụ: Cho cấp số nhân ( Un) có u1 = 6, q = 8. Tính u2?
Trả lời: Ta có: u2 = q.u1 = 8,6 = 48 => u2 = 48.
Kết luận: (u2) = 48.
Số hạng tổng quát của cấp số nhân
Số hạng tổng quát (Un) được xác định theo công thức sau: ( Nhân với số hạng đầu tiên (u1) và bội số q ).
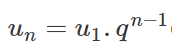
Với n 2
Ví dụ: cho số mũ (Un) có (u1) = 2, q = 5. Tính (u6)
Đáp án: u6 = u1.q^6-1 = 2,5^4 = 1250.
Kết luận: (u6) = 1250.
3. Tính chất của cấp số nhân:
Trong hàm mũ, bình phương của mỗi số hạng (trừ số hạng đầu tiên và số hạng cuối cùng) là tích của hai số hạng liền kề.
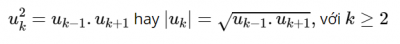
Ví dụ: Cho bốn số a, 10, 20, b theo thứ tự đó tạo thành số mũ. Tìm a và b?
Trả lời: Ta có: 10^2 = a.20 <=> 20 = a.20 => a = 1.
20^2 = 5.b <=> 40 = 5.b => b = 6.
Kết luận: a = 1 và b = 6.
Tổng n của số hạng đầu tiên
Cho một cấp số nhân (Un) có công q khác 1, ta có: Sn = u1 + u2 + u3 +…+ un
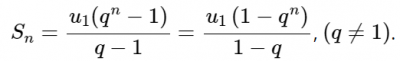
Ví dụ: Cho cấp số nhân (Un) với (u1) = 6 và q = 3. Tính S10?
Trả lời: Ta có: S10 = u1( 1- q^10)/ (1 – q)
<=> S10 = 6( 1 – 3^10 )/ (1-3)
<=> S10 = 6( 3^10 -1)/ 2 (áp dụng công thức tính tổng lũy thừa)
Tổng cấp số nhân lùi vô hạn
Đối với một cấp số nhân lùi vô hạn (U n ) có hệ số q với hệ số q thỏa mãn điều kiện 1 < q < 1 thì được gọi là cấp số nhân lùi vô hạn.
Chúng ta có tổng của cấp số nhân vô hạn ngược S bằng:
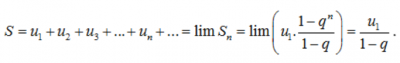
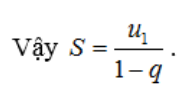
Ví dụ: Tính tổng của cấp số nhân vô cực ngược (Un), có Un = 1/3^n.
Trả lời: Ta có: u1 = 1/2 và u2 = 1/9 => hệ cấp số nhân q = 1/3
Kết luận: S = u1/ (1 – q) = 1/3: (1 – 1/3) = 1/2.
Các dạng bài tập
Dạng 1: Nhận biết cấp số nhân
Phương pháp giải quyết:
– Tính bội số q theo công thức: q = (Un + 1)/ Un (điều kiện n ≥ 1)
– Nếu q là số không đổi thì kết luận rằng dãy (Un) là số mũ. Nếu q thay đổi theo n thì kết luận rằng dãy (Un) không phải là số mũ:
Ví dụ: Cho một số mũ (Un) có số hạng đầu tiên u1 = 8 thì cấp số nhân q = 3. Tìm số hạng thứ 2?
R.54
B.44
C.34
D.24.
Hướng dẫn giải pháp:
Áp dụng công thức hàm mũ Un + 1 = u1.q
Thay u1 = 8 và q = 3 vào công thức trên, ta có: u2 = 8,3 = 24.
Kết luận: Đáp án A. 24 đúng.
Dạng 2: Chứng minh cấp số nhân
Phương pháp giải: Sử dụng tính chất: Ba số hạng u k – 1 ; Vương quốc Anh ; u k + 1 là ba số hạng liên tiếp của cấp số nhân <=> 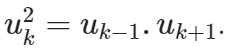
Ví dụ 1: Tìm a, b sao cho các số 5a – b; 2a + 3b; a + 2b tạo thành cấp số cộng và các số (b + 1) 2 ; ab+1; (a – 1) 2 là số mũ?
Hướng dẫn giải pháp:
Theo bài toán ta có các số 5a – b; 2a + 3b; a + 2b tạo thành cấp số cộng
=> Ta có: 2(2a + 3b) = 5a – b + a + 2b
<=> 4a + 6b = 6a + b
<=> 2a = 5b
Theo bài toán ta có các số (b + 1) 2 ; ab+1; (a – 1) 2 là cấp số nhân
=> Ta có: (ab + 1) 2 = (b + 1) 2 (a – 1) 2
<=> [ ab + 1 + (b +1)(a – 1) ] [ ab + 1 – (b +1)(a – 1)] = 0
<=> (2ab – b + a)(2 + b – a) = 0
<=> (4 + 2b – 2a) (4ab + 2a – 2b) = 0
Thay 2a = 5b vào (4 + 2b – 2a) (4ab + 2a – 2b) = 0, ta có:
( 4 + 2b – 5b )( 4ab + 5b – 2b ) = 0
<=> b( 4 – 3b )( 10b + 3 ) = 0
<=> b = 0; b = 4/3; b = -3/10 và a = 0; a = 10/3; một = -3/4
Kết luận ( a; b) ∈ { ( 0; 0 ); ( 10/3; 4/3 ); ( -3/4 ; -3/10) }
Ví dụ 2: Chứng minh ba số x, y, z là số mũ sao cho ba số 2/(x – y) = 1/y = 2/(b – z) tạo thành một số cộng?
Theo bài toán, ba số 2/(x – y) = 1/y = 2/(b – z) tạo thành một cấp số cộng.
Ta có: 2/(x – y) + 2/(y – z) = 2/y
<=> y( y – z + y – x ) = ( y – x )( y – z )
<=> y^2 = xz
Kết luận: Ba số x, y, z tạo thành một số mũ.
Dạng 3: Tìm điều kiện của tham số để bộ số lập thành một cấp số nhân
Phương pháp giải quyết:
– Với điều kiện xz = y^2 thì ba số x, y, z tạo thành một số mũ.
– Với điều kiện xz = y^2 và yh = z^2 thì 4 số x, y, z, h tạo thành một số mũ.
Ví dụ 1: Tìm điều kiện của x sao cho phương trình: ax 2 + hộp 2 + cx + d = 0, trong đó a 0 có 3 nghiệm phân biệt, x 1 .x 2.x 3 tạo thành cấp số nhân.
Hướng dẫn giải pháp:
Giả sử phương trình có ba nghiệm phân biệt x1, x2, x3 tạo thành hàm mũ => x 1x 3 = (x2)^2 ( Điều kiện đủ )
Chúng ta có 😡 1 +x 2 + x 3 = – b/ a và x 1x 2 + x 2x 3 + x 3x 1 = c/ a
<=>x 1x 2 + x 2 lần 3 + (x2)^2 = c/ a
<=>x 2 (x 1 +x 2 + x 3 ) = c/ a
<=>x 2 = – c/ b .
Thay thế x 2 = – c/ b trong phương trình trục 2 + hộp 2 + cx + d = 0, với a ≠ 0 ta có:
a(- c/ b ) ^ 3 + b(- c/ b )^2 + c(- c/ b ) + d = 0
<=> a/c^3 = b^3/d. (Đủ điều kiện)
=> Phương trình có nghiệm x 2 = – c/ b .
Vì vậy: x 2 (x 1 +x 2 + x 3 ) = (- c/ b ) (- b/ a ) = c/ a = x 1x 2 + x 2x 3 + x 3 lần đầu tiên
<=>x 1x 3 = x2 2
<=>x 1 .x 2.x 3 tạo thành cấp số nhân.
Kết luận: Vậy điều kiện cần và đủ của phương trình: ax 2 + hộp 2 + cx + d = 0, trong đó a ≠ 0 có 3 nghiệm hàm mũ khác nhau là a/c^3 = b^3/d.
Lưu ý: Với bài toán tìm tham số m, với điều kiện đủ, có thể khẳng định bằng cách nêu nghiệm cụ thể của phương trình. Vì khi đó ta còn phải chứng minh phương trình đã cho có 3 nghiệm phân biệt.
Ví dụ 2: Cho ba số a – 2, a – 4, a + 2 tạo thành một cấp số nhân. Vậy x bằng bao nhiêu?
Hướng dẫn giải pháp:
Để ba số a – 2, a – 4, a + 2 tạo thành số mũ thì phải thỏa mãn các điều kiện sau:
(a – 4)^2 = (a – 2)(a + 2)
<=> 8a = 20
<=> a = 5 2 .
Kết luận: Với điều kiện a = 5 2 thì ba số a – 2, a – 4, a + 2 tạo thành một số mũ.
Dạng 4: Tìm các phần tử của một cấp số nhân (un)
Phương pháp giải quyết:
– Dãy số (u n ) là số mũ khi và chỉ khi (u n + 1 u n )/ u n = q không phụ thuộc vào n và q là bội số của cấp số nhân (u n )
– Cần xác định số hạng thứ nhất u1 và bội số q. Ta thiết lập hệ phương trình với hai ẩn số u 1 và q. Tìm số hạng đầu tiên u 1 và bội số q.
– Dựa vào công thức tổng quát: u n = u 1 . qn -1 hoặc công thức đệ quy u n = u n – 1 . q. Tìm số hạng n?
Ví dụ 1: Cho một cấp số nhân (u n ) thỏa mãn điều kiện: u1 + u5 = 51 và u2 + u6 = 102. Cho:
a) Xác định số hạng đầu tiên u1 và bội số q?
b) Xác định công thức tổng quát của hàm số mũ (u n )?
c) Tìm số hạng thứ 15, 17, 19 và 21 của dãy số mũ (u n )?
Hướng dẫn giải pháp:
a) Theo bài toán ta có: u1 + u5 = 51 => u1 + u1.q^4 = 51 <=> u1 ( 1 + q^4 ) = 51
và ta có: u2 + u6 = 102 => u1.q + u1.q^5 = 102 <=> u1.q ( 1 + q^4 ) = 102
Lấy cả hai vế của phương trình u1.q ( 1 + q^4 ) = 102 chia cho cả hai vế của phương trình u1 ( 1 + q^4 ) = 51, ta có: [u1.q ( 1 + q^4 ) )] : [ u1 ( 1 + q^4 ) ] = 102 : 51
<=>q=2.
=> u1 = 51/( 1 + q^4 ) = 3
Kết luận: số hạng thứ nhất u1 = 3 và bội số q = 2.
b) Công thức tổng quát của hàm mũ (u n ) là:
u n = u 1 . q n–1 sẽ suy ra u n = 3,2 n–1 .
c) Số hạng thứ 15 của dãy số mũ (u n ) là: u 15 = 3,2 14 = 49152.
Số hạng thứ 17 của dãy số mũ (u n ) là: u 17 = 3.2 16 = 196608.
Số hạng thứ 19 của dãy số mũ (u n ) là: u 19 = 3.2 18 = 786432
Số hạng thứ 21 của dãy số mũ (u n ) là: u 21 = 3.2 20 = 3145728.
Dạng 5: Tính tổng của cấp số nhân
Phương pháp giải quyết:
Đối với thừa số q khác 1 nếu (u n ) là số mũ thì tổng n số hạng đầu tiên của số mũ (u n ) sẽ được xác định theo công thức: S n = [ u1( 1 – q^n ) / (1–q)]
Ví dụ 1: Cho một cấp số nhân (u n ) có số hạng tổng quát là: u n = 2.( –3) k .
a) Tính S 15 Khi cấp số nhân ( un ) có số hạng tổng quát: u n = 2.( –3) k .
b) Tính tổng tất cả các số hạng của số mũ ( un ) khi số hạng đầu tiên của số mũ (u n ) là 18, số hạng thứ hai còn lại là 54 và số hạng cuối cùng là 39366.
Hướng dẫn giải pháp:
a) Khi cấp số nhân (u n ) có số hạng tổng quát là: u n = 2. (– 3) k => số hạng thứ nhất u 1 = 2 và cấp số nhân q = – 3
=> S 15 = [ u1( 1 – q^n ]/ (1 – q) = ( 3^15 + 1) / 2.
b) Số hạng thứ nhất u 1 = 18
Số hạng thứ hai u2 = 54 => u1.q = 54 => cấp số nhân q = 3
Số hạng cuối u n = 39366
=>u1.q^(n – 1)= 39366 <=> 18.3^(n – 1) = 39366 => n = 8.
=> S 8 = [ u1(1 – q)^n]/(1 – q) = 59040.




