Tam giác là một hình học quan trọng, vậy bạn đã biết định nghĩa và tính chất của tam giác chưa? Hãy cùng tìm hiểu qua bài viết dưới đây nhé!
Hình tam giác là gì?
Hình tam giác là một loại hình học cơ bản trong đó ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh. Tam giác là đa giác đều và là đa giác có ít cạnh nhất (3 cạnh). Tổng ba góc của một tam giác là 180 độ.
– Tam giác là hình gồm có 3 điểm không thẳng hàng, 3 cạnh là 3 đoạn thẳng nối các đỉnh với nhau. Tam giác có 3 cạnh, 3 đỉnh và 3 góc.
– Chủ đề này giúp học sinh biết cách tính chu vi, diện tích hình tam giác. Hoặc tìm chiều cao (cạnh dưới) khi biết diện tích, cạnh dưới (chiều cao).
Dấu hiệu phân biệt hình tam giác
- Một tam giác vuông sẽ có một góc vuông.
- Tam giác có hai góc nhọn phụ nhau là tam giác vuông.
- Tam giác có đường trung tuyến bằng nửa cạnh là tam giác vuông.
- Tam giác có bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh kia là tam giác vuông.
- Nếu một tam giác nội tiếp trong một đường tròn có đường kính các cạnh thì tam giác đó là tam giác vuông.
Phân loại hình tam giác
Tam giác tù
Tam giác tù là tam giác có góc trong lớn hơn 90 độ.
Góc a là góc tù, góc b và c là góc nhọn.
Tam giác vuông
Tam giác vuông là tam giác có một góc bằng 90 độ. Cạnh huyền là cạnh dài nhất của một tam giác vuông.
Trong hình minh họa trên, góc a = 90 độ trong khi góc b và c là góc nhọn.
Tam giác cân
Tam giác cân là tam giác có hai cạnh và hai góc bằng nhau. Độ dài bằng nhau của một tam giác được thể hiện bằng cách tạo thành một vòng cung ở mỗi cạnh.
Trong sơ đồ trên, độ dài cạnh AB = AC và ∠ ABC = ∠ ACB.
Tam giác đều
Một tam giác đều có ba cạnh bằng nhau và ba góc trong bằng nhau. Trong trường hợp này, mỗi góc trong của một tam giác đều có số đo là 60 độ. Tam giác đều đôi khi được gọi là tam giác đều vì cả ba góc đều bằng nhau.
Trong một tam giác đều, cạnh AB = BC = AC và ABC = ACB = BAC
Lưu ý rằng các góc của một tam giác đều không phụ thuộc vào độ dài các cạnh.
Tính chất của hình tam giác
- Tổng 3 góc trong một tam giác là 180 độ
- Số đo của một góc ngoài bằng tổng số đo của hai góc trong không kề với nó.
Bài tập áp dụng
Dạng 1: Tính chu vi tam giác:
Phương pháp giải quyết
– Để tính chu vi hình tam giác, ta tính tổng độ dài 3 cạnh.
– Công thức: C = a + b + c (C: chu vi; a, b, c: chiều dài 3 cạnh bằng 1 đơn vị đo)
Bài tập minh họa
Bài 1: Tính chu vi tam giác ABC biết AB = 3cm, BC = 4cm, AC = 5cm.
Hướng dẫn giải pháp
Chu vi tam giác ABC là:
3+4+5=12(cm)
Đáp án: 12cm
Bài 2: Tính cạnh BC của tam giác ABC biết chu vi tam giác ABC là 25 cm, cạnh AB = 10 cm, AC = 7 cm.
Hướng dẫn giải pháp
Độ dài cạnh BC của tam giác ABC là:
25 – 10 – 7 = 8 (cm)
Đáp án: 8cm
Dạng 2: Tính diện tích tam giác:
Phương pháp giải quyết
Để tính diện tích hình tam giác, chúng ta cần xác định chiều cao và đáy của hình tam giác tương ứng. 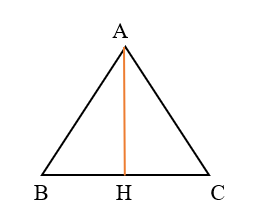
– Tam giác ABC có AH là đường cao, BC là đáy, ứng với đường cao AH
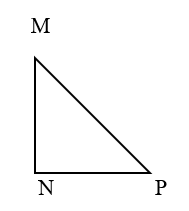
– Tam giác MNP là tam giác vuông nên hai cạnh vuông góc MN và NP lần lượt là chiều cao và chiều dài đáy.
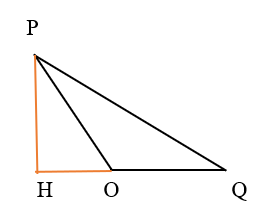
– Tam giác POQ có PH là đường cao, OQ là độ dài đáy tương ứng với đường cao PH. (Vì tam giác POQ là tam giác có 1 góc tù nên khi tính diện tích ta cần vẽ đường cao bên ngoài tam giác)
– Để tính diện tích hình tam giác, ta nhân độ dài đáy với chiều cao (cùng đơn vị đo) rồi chia cho 2.
– Công thức tính diện tích tam giác: S=ax h2″> S = a X h 2 S=ax h2
(S: diện tích; a là chiều dài đáy; h là chiều cao)
– Tính chiều cao khi biết diện tích và chiều dài đáy: h = 2xS: a
– Tính độ dài đáy khi biết diện tích và chiều cao: a = 2xS : h
Bài tập minh họa
Bài 1: Tính diện tích tam giác ABC có chiều dài đáy 5m và chiều cao 3m.
Hướng dẫn giải pháp
Diện tích tam giác ABC là:
(5×3): 2 = 7,5 ( m2 )
Đáp số: 7,5 m 2
Bài 2: Tính chiều cao AH của tam giác ABC khi biết diện tích tam giác là 20 cm 2 và chiều dài đáy là 8 cm.
Hướng dẫn giải pháp
Độ dài đường cao AH là:
2×20: 8 = 5 (cm)
Đáp án: 5cm




