Biết được dấu và tính chất đặc biệt của tam giác đều sẽ giúp học sinh tự tin nắm vững những kiến thức cần thiết để giải các bài toán. Bài viết dưới đây cung cấp cho các bạn những kiến thức quan trọng về tam giác đều trong chương trình toán đại học.
Tam giác đều là gì?
Trong hình học, tam giác đều là tam giác có ba cạnh bằng nhau hoặc tương đương và ba góc bằng 60°. Đó là một đa giác đều có các cạnh bằng 3.
Cho tam giác đều ABC có AB = AC = BC.
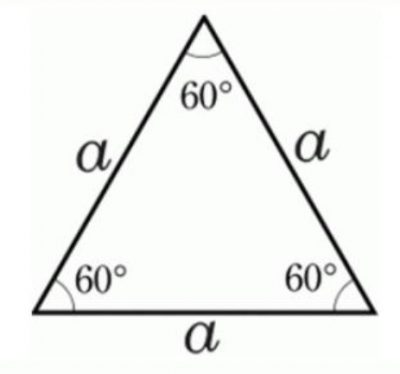
Kết quả:
Trong một tam giác đều, mỗi góc bằng 60°.
– Tam giác có 3 góc bằng nhau là tam giác đều.
– Tam giác cân có một góc bằng 60° là tam giác đều.
Dấu hiệu nhận biết tam giác đều
– Tam giác có ba cạnh bằng nhau là tam giác đều
– Tam giác có ba góc bằng nhau là tam giác đều
– Tam giác cân có một góc bằng 60 0 là tam giác đều
– Tam giác có hai góc bằng 60 0 là tam giác đều
Cách chứng minh tam giác đều:
Cách 1: Chứng minh tam giác có 3 cạnh bằng nhau.
Ví dụ: Tam giác OAB có OA = OB = AB
=> tam giác đều OAB
Cách 2: Chứng minh tam giác có 3 góc bằng nhau.
Ví dụ: Chứng minh tam giác OAB có góc O = B = A
=> tam giác đều OAB
Cách 3: Chứng minh tam giác cân và có một góc bằng 60 độ.
Ví dụ: tam giác OAB có OA = OB và Cell = 60°
=> tam giác đều OAB
Cách 4: Chứng minh tam giác có 2 góc bằng 60 độ.
Ví dụ: Tam giác OAB có góc A = B = 60°
=> tam giác đều OAB
Tính chất của tam giác đều
Trong một tam giác đều, mỗi góc bằng 60 độ.
Cho tam giác ABC: góc A = góc B = góc C = 60 độ
Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
Cho tam giác ABC đều: góc A = góc B = góc C
Nếu một tam giác cân có một góc bằng 60 độ thì tam giác này là tam giác đều.
Trong một tam giác đều, đường trung tuyến vừa là đường cao vừa là đường phân giác của tam giác đó.
Cho tam giác đều ABC, AD là đường trung tuyến vẽ đỉnh A. Khi đó AD là đường cao và đường phân giác của tam giác ABC.
Cách dựng tam giác đều:
Cách dựng tam giác đều ABC
– Vẽ cạnh BC
– Vẽ (B; BC) và (C; BC)
– (B; BC) (C; BC) trong A
ABC là tam giác đều cần vẽ.
Trọng tâm của tam giác:
Tính chất trọng tâm của tam giác là: Khoảng cách từ trọng tâm đến ba đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
Giả sử tam giác ABC có 3 đường trung tuyến AM, BN, CP với G là trọng tâm như hình vẽ. Theo tính chất trên ta có:
– GA = 2/3 sáng
– GB = 2/3 NĂM
– GC = 2/3 CP
Cho tam giác đều ABC có G là giao điểm của ba đường trung tuyến của ba đỉnh. Khi đó, G đồng thời là trọng tâm, trực tâm, tâm đường tròn nội tiếp và tâm đường tròn ngoại tiếp tam giác ABC.
Công thức tam giác đều
Công thức tính diện tích tam giác đều
Diện tích của một tam giác đều bằng 1/2 tích của đáy nhân với chiều cao, công thức là:
S = 1/2 (axh)
Trong đó:
S là diện tích của tam giác
a là độ dài cạnh đáy
h là chiều cao
Ví dụ: Để tính diện tích tam giác đều:
a, Chiều dài một cạnh của tam giác là 6 cm và chiều cao là 10 cm.
b, Độ dài một cạnh của tam giác là 4 cm và chiều cao là 5 cm.
Trả lời:
a, Diện tích tam giác là: (6 x 10): 2 = 30 (cm.)2)
Đáp số: 30 cm2
b, Diện tích tam giác là: (4 x 5): 2 = 10 (cm2)
Đáp số: 10 cm2
Lưu ý khi tính diện tích hình tam giác:
– Với tam giác có một góc phẳng thì chiều cao nằm ngoài tam giác nên độ dài cạnh cần tính diện tích chính bằng độ dài cạnh bên trong tam giác.
– Khi tính diện tích hình tam giác, chiều cao tương ứng với đáy này là bao nhiêu.
– Nếu hai tam giác có cùng chiều cao hoặc có cùng chiều cao thì suy ra diện tích của hai tam giác tỉ lệ với hai đáy và ngược lại nếu hai tam giác có cùng đáy (hoặc hai đáy bằng nhau) , tính diện tích tích của tam giác tỉ lệ với 2 đường cao tương ứng.
Công thức tính chu vi tam giác đều
Chu vi của một tam giác đều bằng tổng ba cạnh của tam giác đó, công thức:
P = a + a + a hoặc P = 3 xa
Trong đó:
P là chu vi của tam giác
a là cạnh của tam giác
Ví dụ: Tính chu vi tam giác đều ABC có cạnh AB = 5 cm
Trả lời:
=> Vì tam giác ABC là tam giác đều nên ta có độ dài các cạnh là: AB = AC = BC = 5cm
Theo công thức tính chu vi tam giác đều ta có: P(ABC) = 5 x 3 = 15cm
Bán kính hình tròn nội tiếp tam giác đều:
r = ax 3 / 6
Bán kính đường tròn ngoại tiếp tam giác đều:
R = ax √3 / 3
Công thức tính đường cao của tam giác đều
Trong một tam giác đều, đường cao vừa là đường phân giác, vừa là đường trung tuyến
Biểu thức: h = ax 3/2
Trong đó:
a là độ dài cạnh của một tam giác đều
h là chiều cao của hình tam giác
AD = CF (gt)
Góc A = Góc B (vì ABC chẵn)
EC = AF (đã chứng minh ở trên)
Suy ra: ∆ADF = CFE (cạnh – góc – cạnh)
Suy ra: DF = FE (hai cạnh tương ứng) (7)
Từ (6) và (7) suy ra: DF = ED = FE
Vậy ∆DEF là số chẵn.
Ví dụ 4 : Vẽ tam giác đều ABC có cạnh 4 cm.
Giá:
– Vẽ đoạn thẳng BC = 4 cm
– Vẽ cung tròn tâm B bán kính 4 cm.
– Vẽ đường tròn tâm C bán kính 4 cm.
– Hai cung này cắt nhau tại A.
– Nối AB, AC ta vẽ được tam giác ABC.
Ví dụ 5: Chứng minh hình dưới đây là tam giác đều
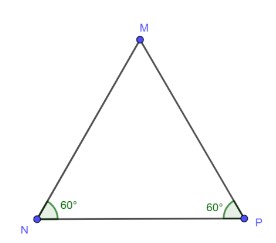
Áp dụng định lý tổng ba góc trong tam giác MNP, ta có:
Góc M + Góc N + Góc P = 180 độ
Từ hình vẽ, Góc N = Góc P = 60 độ
Suy ra: Góc M = 180 – 60 – 60 = 60 độ
Suy ra: Góc M = Góc N = Góc P = 60 độ
Vậy tam giác MNP là tam giác đều vì có ba góc bằng nhau.
Bài tập ứng dụng
Bài 1: Cho ΔABC là góc B = 60°, AB = 2 cm, BC = 5 cm. Trên cạnh BC lấy điểm D sao cho BA = BD
a) Chứng minh tam giác ABD là tam giác đều
b) Gọi H là trung điểm của BD. Bằng chứng về AH⊥BD
c) Tính độ dài AC
Bài 2: Cho tam giác ABC vuông tại A với 
. Vẽ Cx vuông góc với BC, trên bán kính Cx lấy điểm E sao cho CE = CA (CE , CA cùng phía đối diện BC). trên bán kính đối diện của bán kính BC lấy điểm F sao cho BF = BA. Chứng minh :
MỘT. ACE Tam giác đều
b. A, E, F thẳng hàng.
Bài 3: Cho sáu hình tam giác đều có cùng độ dài một cạnh là 3 cm, độ dài cạnh của hình lục giác đều là bao nhiêu?
R. 3 cm
b.6cm
C.9cm
D.12cm
Bài 4: “Số đo các góc của một lục giác đều…số đo các góc của một tam giác đều”. Điền từ còn thiếu vào chỗ trống để được câu đúng.
A. bằng nhau.
B.nhân đôi.
C. nhỏ hơn.
D. lớn hơn.
Trên đây là tổng hợp những kiến thức liên quan đến tam giác đều. Chúng tôi hy vọng nó sẽ hữu ích cho các em trên hành trình làm chủ kiến thức của mình.




