Đường cao là một đường quan trọng trong một tam giác và có liên quan mật thiết đến các bài toán hình học phẳng. Vậy Đường cao là gì? Làm thế nào để tính độ cao trong một hình tam giác? Tính chất đường cao trong một tam giác là gì?
Đường cao là gì?
Đường cao của một tam giác là đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện của tam giác.
- Cạnh đối diện được gọi là đáy tương ứng với độ cao này.
- Phần giao nhau giữa đáy và đỉnh gọi là chân trên.
- Độ dài đỉnh được tính bằng khoảng cách từ trên xuống dưới.
Trong một tam giác sẽ có 3 đường cao hạ dần từ 3 đỉnh của tam giác đó. Ba đường cao này sẽ hội tụ (giao nhau) tại một điểm. Điểm này được gọi là trực tâm.
Trực tâm của một tam giác có thể là bên trong (xuất hiện trong tam giác nhọn) hoặc bên ngoài (xuất hiện trong tam giác tù) hoặc trùng với một đỉnh của tam giác (xuất hiện trong tam giác vuông).
Lưu ý: Tính chất ba đường cao của tam giác áp dụng theo định lý: Ba đường cao của tam giác cùng đi qua một điểm. Điểm này gọi là trực tâm của tam giác
Tính chất đường cao trong tam giác
Tính chất đường cao trong tam giác cân
Trong một tam giác cân, theo định nghĩa, đường cao tương ứng với đáy là đường trung bình của đáy này. Như vậy, chiều cao của tam giác cân đi qua điểm giữa của đáy. Hơn nữa, chiều cao của một tam giác cân còn là đường phân giác của góc ở đỉnh và là đường phân giác của đáy tam giác. Ngược lại, nếu một tam giác có đường cao và cũng là đường trung tuyến hoặc đường phân giác thì tam giác đó là tam giác cân.
Lưu ý: Tam giác đều là một dạng đặc biệt của tam giác cân. Do đó, tính chất độ cao trong một tam giác đều cũng giống như tính chất độ cao trong tam giác cân.
Tính chất đường cao trong tam giác vuông
Trong một tam giác vuông, đường cao có đáy của một góc vuông là cạnh kia của góc vuông. Như vậy, đỉnh của góc vuông là chân đường cao tính từ hai đỉnh còn lại đến hai góc vuông của tam giác.
Tính chất các đường cao của tam giác vuông cân
Tam giác vuông cân vừa là tam giác vuông vừa là tam giác cân. Đường cao trong tam giác vuông cân cũng là đường phân giác, đường trung tuyến tính từ đỉnh của góc vuông của tam giác. Ngoài ra, độ dài đường cao tính từ đỉnh của góc vuông sẽ bằng một nửa độ dài cạnh huyền.
Công thức tính đường cao trong tam giác
Công thức tính đường cao trong tam giác thường
Cách tính độ cao trong tam giác bằng công thức Hero:
trong đó a, b, c là độ dài các cạnh; ha là độ cao nhìn từ đỉnh A đến cạnh BC; p là nửa chu vi:
p = (a + b + c): 2
Ví dụ:
Cho tam giác ABC có cạnh AB = 4 cm, cạnh BC = 7 cm, cạnh AC = 5 cm. Tìm đường cao AH vì A cắt BC tại H và tính diện tích ABC.
Giá:
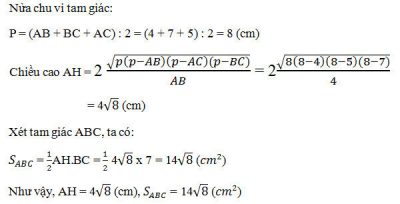
Công thức tính đường cao trong tam giác cân
Giả sử bạn có tam giác cân ABC tại A, đường cao AH vuông góc với H như hình trên:
Công thức tính độ cao AH:
Vì tam giác ABC cân tại A nên đường cao AH cũng là đường trung bình nên:
HB=HC=BC
Áp dụng định lý Pytago cho tam giác vuông ABH tại H, ta có:
AH2+BH2=AB2
⇒AH2=AB2-BH2
Ví dụ: Cho Δ ABC cân bằng tại A có BC = 30 cm, chiều cao AH = 20 (cm). Tính độ cao tương ứng với cạnh của tam giác cân này.
Giải: Cho ABC cân bằng tại A có BC = 30( cm )
⇒ BH = CH = 15( cm ).
Áp dụng định lý Py-ta-go, ta có:

Công thức tính đường cao trong tam giác đều
Công thức:
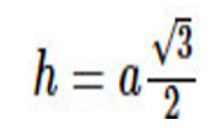
Trong đó: h là chiều cao của tam giác đều
a là độ dài cạnh của một tam giác đều
Công thức tính đường cao trong tam giác vuông
Giả sử có tam giác vuông ABC, vuông tại A như hình vẽ:
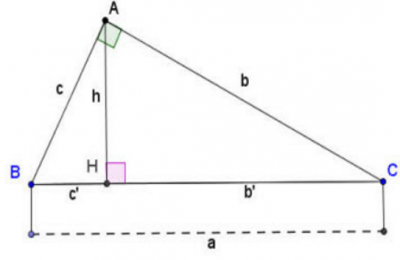
Công thức tính cạnh và đường cao của tam giác vuông:
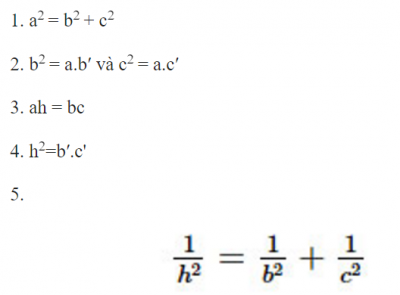
Trong đó: a, b, c lần lượt là các cạnh của tam giác vuông như hình trên;
b’ là hình chiếu của cạnh b lên cạnh huyền;
đó là hình chiếu của cạnh c lên cạnh huyền;
h là chiều cao của tam giác vuông vẽ từ đỉnh góc vuông A đến cạnh huyền BC.
Các công thức toán học thông dụng về độ cao trong tam giác
Các dạng toán thông dụng
Dạng 1: Chứng minh hai đường thẳng vuông góc
Phương pháp:
Sử dụng tính chất trực tâm của tam giác.
Nếu H là giao điểm của hai đường cao kẻ từ B và C kẻ từ ABC thì AH ⊥ BC
Loại 2: Bài toán về độ cao của tam giác, tam giác cân, tam giác đều
Phương pháp:
– Dùng độ cao vuông góc với phía đối diện
– Sử dụng định lý “Trong một tam giác cân, đường cao tương ứng với đáy cũng là đường phân giác, đường trung tuyến và đường trung trực của tam giác này” sao cho một trong các đường trung tuyến, đường phân giác và đường cao, đường trung tuyến ứng với cạnh dưới cũng khớp với các dòng còn lại.
– Nhận xét: Trong một tam giác, nếu hai trong bốn loại đường thẳng (trung tuyến, phân giác, trực giao và đường cao) trùng nhau thì tam giác đó là tam giác cân.
Dạng 3: Chứng minh ba đường thẳng đồng quy
Phương pháp:
Nếu ba đường thẳng đó là đường cao của một tam giác thì chúng cùng đi qua một điểm.
Một số bài tập
Bài 1: Cho tam giác đều ABC, cạnh AB = BC = AC = a = 6, vẽ đường cao của A hướng xuống cắt BC tại H, tính chiều cao AH.
Giải:

Bài 2: Cho tam giác vuông ABC tại A, AB=24cm, AC=32cm. Đường trung trực của BC cắt AC, BC theo thứ tự D và E. Tính DE.
Giải:
Xét tam giác vuông ABC, ta có:
BC2 = AB2+ AC2 (theo định lý Pythagore)
BC2 = 242+ 322
BC2 = 1600
BC=40(cm)
CE=BC:2=40:2=20(cm)
Xét tam giác vuông ACB và tam giác vuông ECD:
Có A = ∠E = 90o
C chung
=> Tam giác ACB Tam giác ECD (gg)
=> AC/EC = AB/ED
=> ED = AB.EC/AC = 15cm
Vậy DE = 15cm
Bài 3: Cho tam giác ABC có góc A = 70, AB < AC, phân giác của góc A cắt BC tại D, BF vuông góc với AC tại F, E thuộc AC sao cho AE = AB. Xác định trực tâm tam giác ABE và tính góc DHF.
Hướng dẫn giải pháp:
Giả sử AD cắt BE = I.
Vì AB = AE nên tam giác ABE cân tại A.
Mặt khác AD là phân giác góc A của tam giác ABC.
=> AI là đường cao của tam giác ABE
BF vuông góc với AE => BF là đường cao tam giác ABE
Vì BF cắt AI = H nên H là trực tâm tam giác ABE
Xét tam giác HEF có: góc FHE = 90 – góc FEH (1)
Xét tam giác HIE có góc EHI = 90 – IEH (2)
Từ (1) và (2) ta có: góc FHD = góc FHE + góc EHI = 180 – góc FEH – góc IEH = 180 – góc FEI
Vì tam giác ABE cân tại A nên góc AEB = góc ABE = (180 – góc BAE)/2 = (180 – 70)/2 = 55
=> Góc EHD = 180 – Góc FEI = 180 – 55 = 125
Bài 4. Cho tam giác ABC có góc A > 90. AD vuông góc với BC tại D, BE vuông góc với AC tại E. Gọi F là giao điểm của AD và BE. Chứng minh AB vuông góc với FC
Hướng dẫn giải pháp:
Xét tam giác FBC có:
AD vuông góc với BC nên FD vuông góc với BC (1)
BE vuông góc với AC => CE vuông góc với BF (2)
Từ (1) và (2) suy ra CE và FD là các đường cao của tam giác FBC mà FD cắt CE = A nên A là trực tâm tam giác FBC.
=> A thuộc đường cao hạ từ B của tam giác FBC => AB vuông góc với FC
Bài tập 5. Cho tam giác cân ABC tại A. Trên cạnh AB lấy điểm D bất kỳ (D#A,B), trên bán kính đối diện của bán kính AC lấy điểm E sao cho AD = AE. Chứng minh ED vuông góc với BC.
Hướng dẫn giải pháp:
Xét tam giác ABE và tam giác ACD có:
AE = AD
góc BAE = góc CAD = 90
AB = AC
Vậy tam giác ABE = tam giác ACD(cgc)
=> góc ACD = góc ABE (hai góc tương ứng) (1)
Gọi F là giao điểm của CD và BE
Ta có, góc FDB = góc ADC (hai góc đối đỉnh) (2)
Góc ADC + góc DCA = 90 (3)
Từ (1), (2) và (3) ta có: góc FDB + góc FBD = góc ADC + góc DCA = 90
Trong tam giác FDB có:
góc DFB = 180 -(góc FDB + góc FBD) = 180 -90 = 90
=> CD vuông góc BE
Xét tam giác BEC có:
AB vuông góc EC
CD vuông góc BE
CD đó cắt AB = D
Vậy D là trực tâm tam giác BEC
Bài tập 6. Cho tam giác vuông ABC tại A. Từ cạnh AC lấy điểm M (M#A, C). Qua M vẽ đường thẳng vuông góc với BC tại N. Từ C vẽ đường thẳng vuông góc với BM tại P. Chứng minh ba đường thẳng AB, CP, MN cùng đi qua một điểm
Hướng dẫn giải pháp:
Gọi D là giao điểm của AB và CP.
Xét tam giác DBC có:
AB vuông góc với AC => AC vuông góc với BD (1)
CP vuông góc với BP => BP vuông góc với DC (2)
Từ (1) và (2) suy ra CA và BP là đường cao của tam giác DBC
trong đó BP cắt AC = m nên M là trực tâm tam giác DBC => DM vuông góc với BC
Lại MN vuông góc với BC nên M, N, D thẳng hàng => AB, MN và CP cùng đi qua điểm D
Bài 7. Cho tam giác ABC cân tại A. M là trung điểm BC, đường cao CN cắt AM tại H. Chứng minh BH vuông góc với AC.
Hướng dẫn giải pháp:
Vì tam giác ABC cân tại A và M là trung điểm của BC nên Am vừa là đường trung tuyến vừa là đường cao tương ứng với BC.
=> AM vuông góc với BC.
Ngược lại CN vuông góc với AB, AM cắt CN = H
=> H là trực tâm tam giác ABC
=> BH thuộc đường cao B của tam giác ABC
=> BH vuông góc với AC
Bài tập 8. Cho tam giác ANC, góc A = 100, góc C = 30, đường cao AH. Trên cạnh AC lấy điểm D sao cho góc CBD = 10. Vẽ đường phân giác của góc BAD cắt BC tại E. Chứng minh AE vuông góc với BD.
Hướng dẫn giải pháp:
Vì góc ADB là góc ngoài của tam giác DBC nên:
góc ADB = góc DBC + góc DCB = 10 + 30 = 40
Trong tam giác ABC có:
góc ABC = 180 – góc BAC – góc ACB = 180 – 100 – 30 = 50
góc ABD = góc ABC – góc DBC = 50 -10 = 40
Xét tam giác ABD có góc ABC = góc ABD = 40 => tam giác ABD cân tại A
Gọi I là giao điểm của AE và BD thì AI là phân giác của góc BAD.
Vì tam giác ABD cân nên AI cũng là đường cao của tam giác ABD => AI vuông góc với BD hoặc AE vuông góc với DB.
Tìm trực tâm tam giác
Trung tâm trực tiếp là gì?
Trực tâm của một tam giác chỉ đơn giản là giao điểm của ba đường cao xuất phát từ ba đỉnh của tam giác và đồng thời vuông góc với cạnh đối diện. Ba đường cao này sẽ cắt nhau tại một điểm mà chúng ta gọi là trực tâm của tam giác.
Đối với tam giác nhọn: trực tâm sẽ nằm trong vùng bên trong tam giác này.
Đối với tam giác vuông: Trực tâm sẽ là đỉnh của góc vuông.
Đối với tam giác tù: Trực tâm nằm ngoài tam giác.
Tính chất của trực tâm:
Trực tâm của một tam giác là gì? Đây là câu hỏi được nhiều học sinh quan tâm. Hãy tìm hiểu tính chất trực tâm của tam giác dưới đây:
– Trong một tam giác đều, trực tâm vừa là trọng tâm, vừa là tâm của đường tròn ngoại tiếp tam giác này.
– Theo định lý Carnot: Một đường cao vẽ từ một đỉnh của một tam giác cắt đường tròn ngoại tiếp tam giác này tại điểm thứ hai là điểm đối xứng của trực tâm với đáy tương ứng.
– Khoảng cách từ một điểm đến trực tâm của tam giác sẽ gấp đôi khoảng cách giữa tâm đường tròn ngoại tiếp tam giác này và cạnh nối của hai đỉnh còn lại.




